Методы трехмерной реконструкции объектов по изображениям

Важная практическая задача — реконструировать форму и текстуру трехмерного объекта по изображениям. Такая задача используется:

в производстве — роботам, которые работают с трехмерными объектами, надо знать, где находятся части их корпуса в пространстве;
в киноиндустрии;
в обеспечении безопасности (например, блокировка телефона);
в очках виртуальной реальности, где очкам нужно учитывать ваше положение;
в автомобилях.

Классические методы реконструкции 3D раскрываются в книге «Multiple View Geometry in Computer Vision». Она сложная для понимания, но целиком охватывает тему:

Для того, чтобы понимать, как по изображениям восстановить трехмерный мир, сперва нужно определиться с тем, как трехмерный мир проектируется на изображение.

Принцип работы Pinhole camera

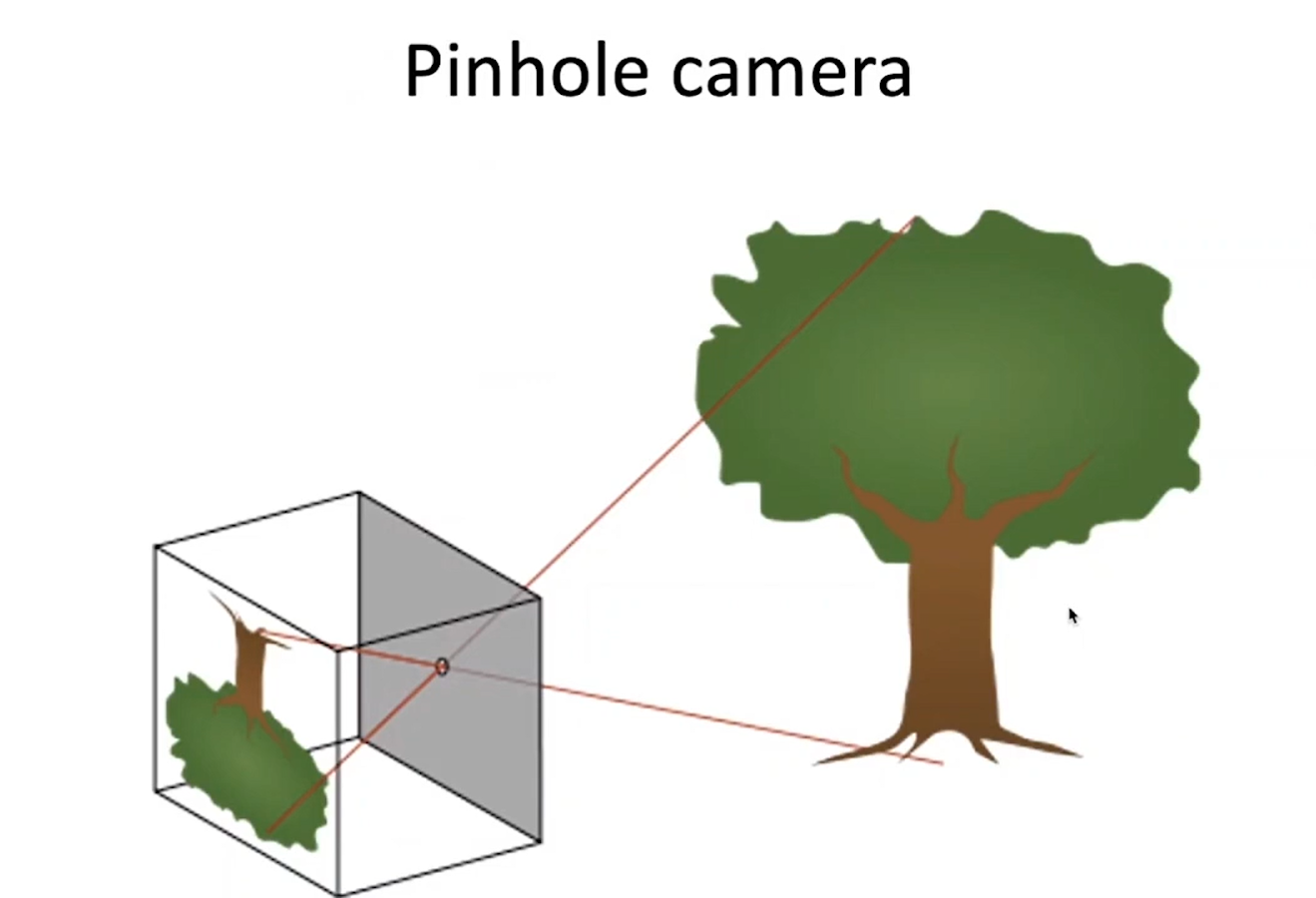
Стандартная модель, которая используется для таких целей, называется Pinhole camera или Camera obscura. Она работает по следующему принципу: каждому пикселю на изображении соответствует ровно один луч в трехмерном пространстве, соединяющий пиксель с маленькой дырочкой, которая называется апертура. Выбранная трехмерная точка может лежать только на этом луче и нигде больше. Этот принцип очень удобен, так как если у нас есть две камеры, и мы знаем взаимное расположение этих камер, то мы можем искать по ним трехмерные точки.

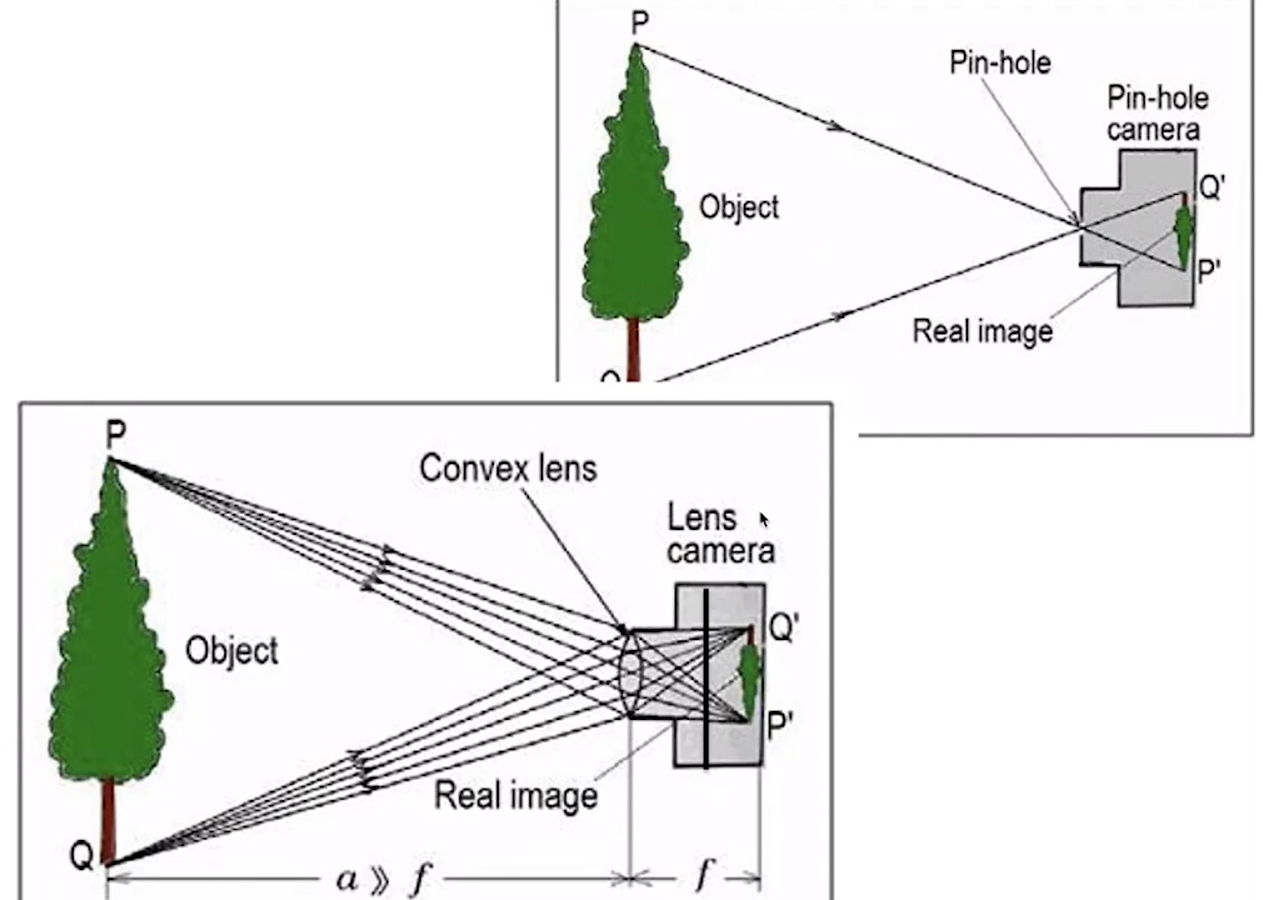
Очевидно, что принцип работает только для маленьких апертур, но не для больших: если наш объект находится не в фокусе, то трехмерная точка линзой с конечной апертурой соберется не в точку, а в некое пятно. Изображение получится размытым, что соответствует такой категории, как глубина резкости.

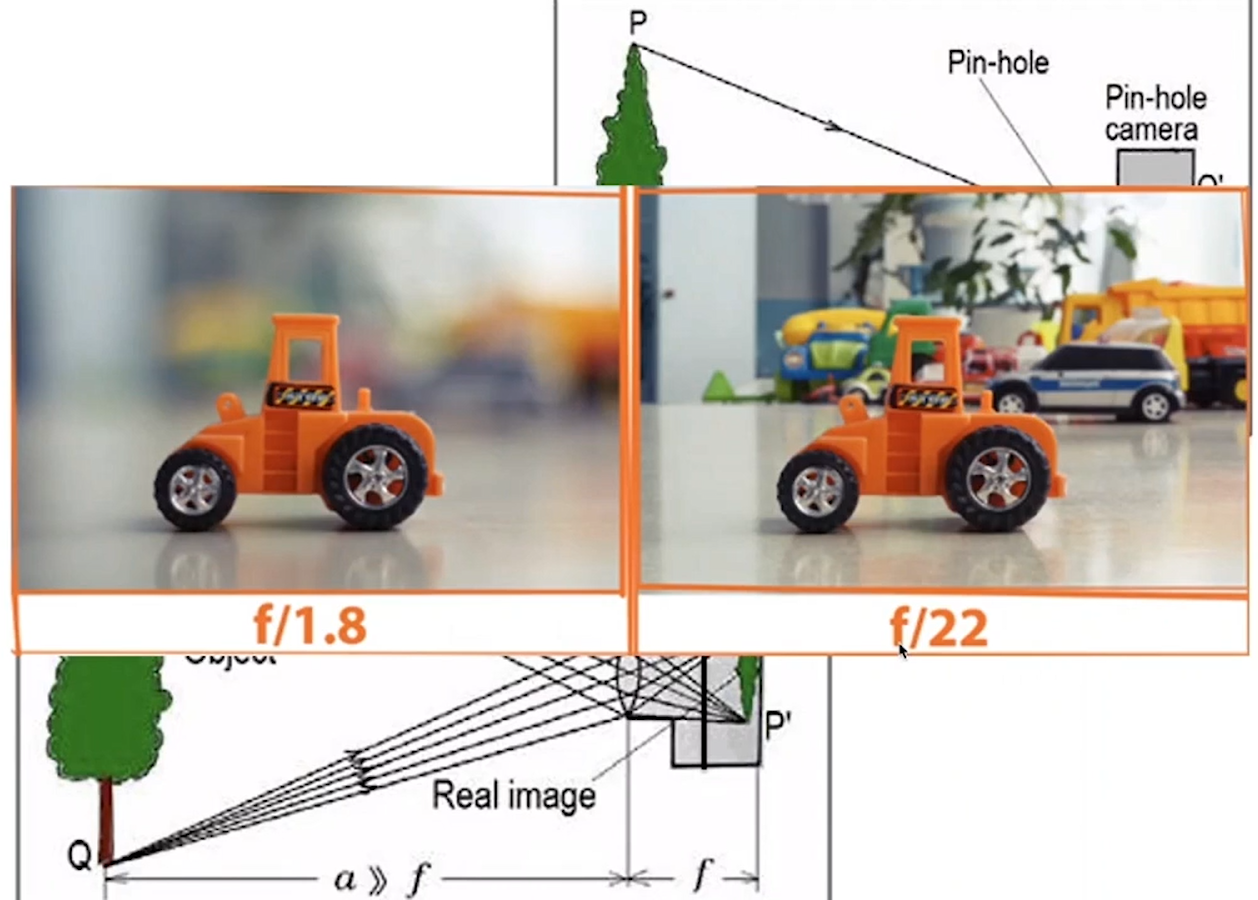
Большинство камер, с которыми мы работаем, хорошо удовлетворяют приближение к Pinhole camera, но в кино и при спортивных соревнованиях, где используются камеры с большими апертурами, принцип работы немного другой.

Система преобразований в Pinhole camera

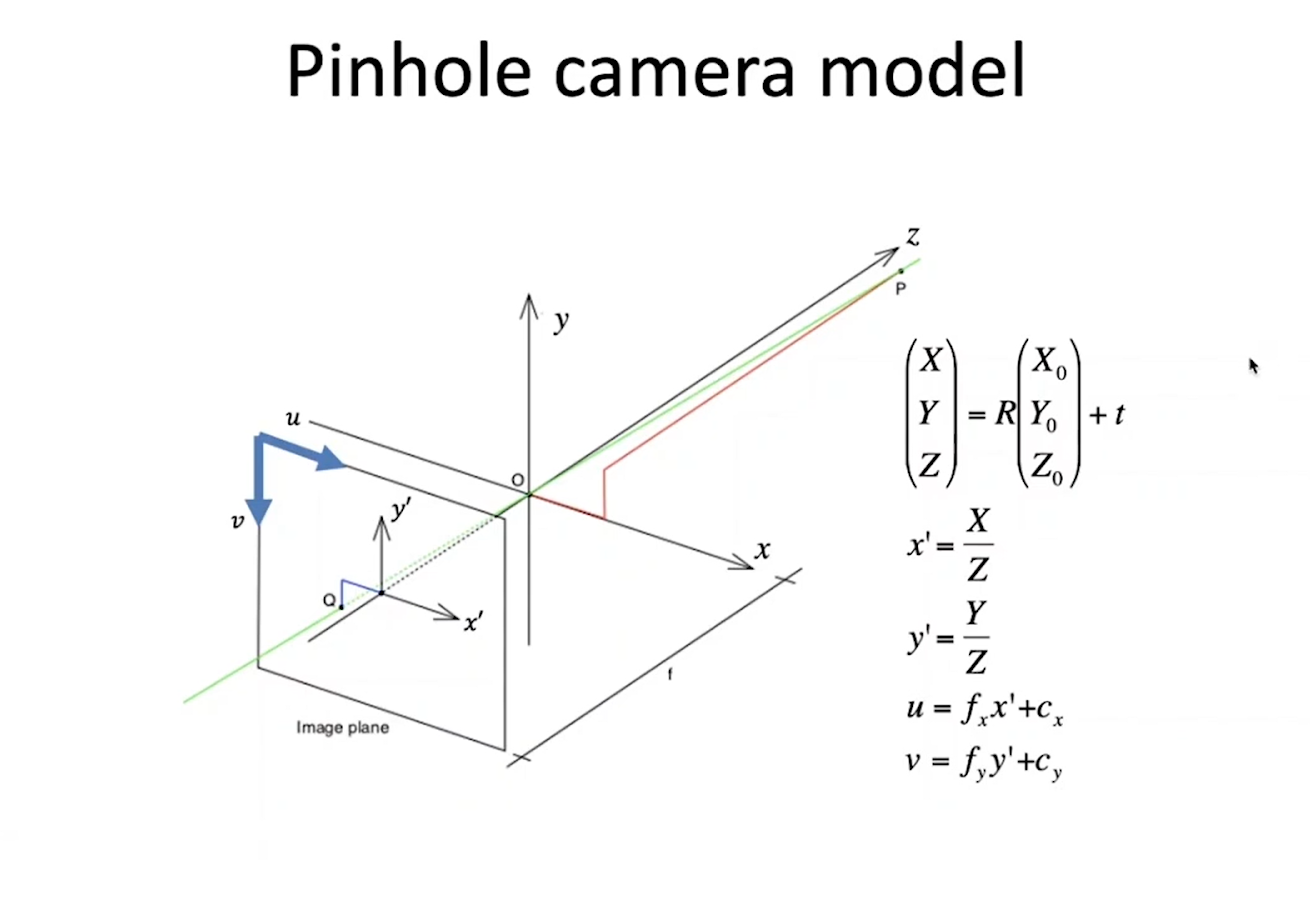
Дальше мы будем говорить именно о Pinhole camera. В ней систему преобразований от трехмерной точки к пикселю можно описать следующим образом – для начала возьмем точку в трехмерном пространстве с координатами X0, Y0, Z0 (в мировой системе отсчета). Камера и мировая система координат связаны между собой через поворот и трансляцию, и любую трехмерную точку перевести в систему координат можно умножением на ортогональную матрицу, которая описывает оборот, и прибавлением вектора трансляций. Получаются координаты X, Y, Z, после получения которых подобными треугольниками легко можно вычислить координаты x’ , y’ уже в плоскости изображения. Для того, чтобы перевести их в координаты пикселей надо умножить координаты на fx, fy и прибавить x, y. fx, fy подразумевают под собой фокусное расстояние; отношение между ними задается сторонами одного пикселя, а cx и cy – это координаты пикселя, через которые проходит оптическая ось. Эти четыре числа называются внутренними параметрами камеры.

Свойства проекции в Pinhole camera:

прямые линии в трехмерном пространстве проецируются в прямые линии на изображении;
параллельные линии в трехмерном пространстве проектируются в пересекающие линии, словно рельсы, которые пересекаются на границах.

Проективная геометрия

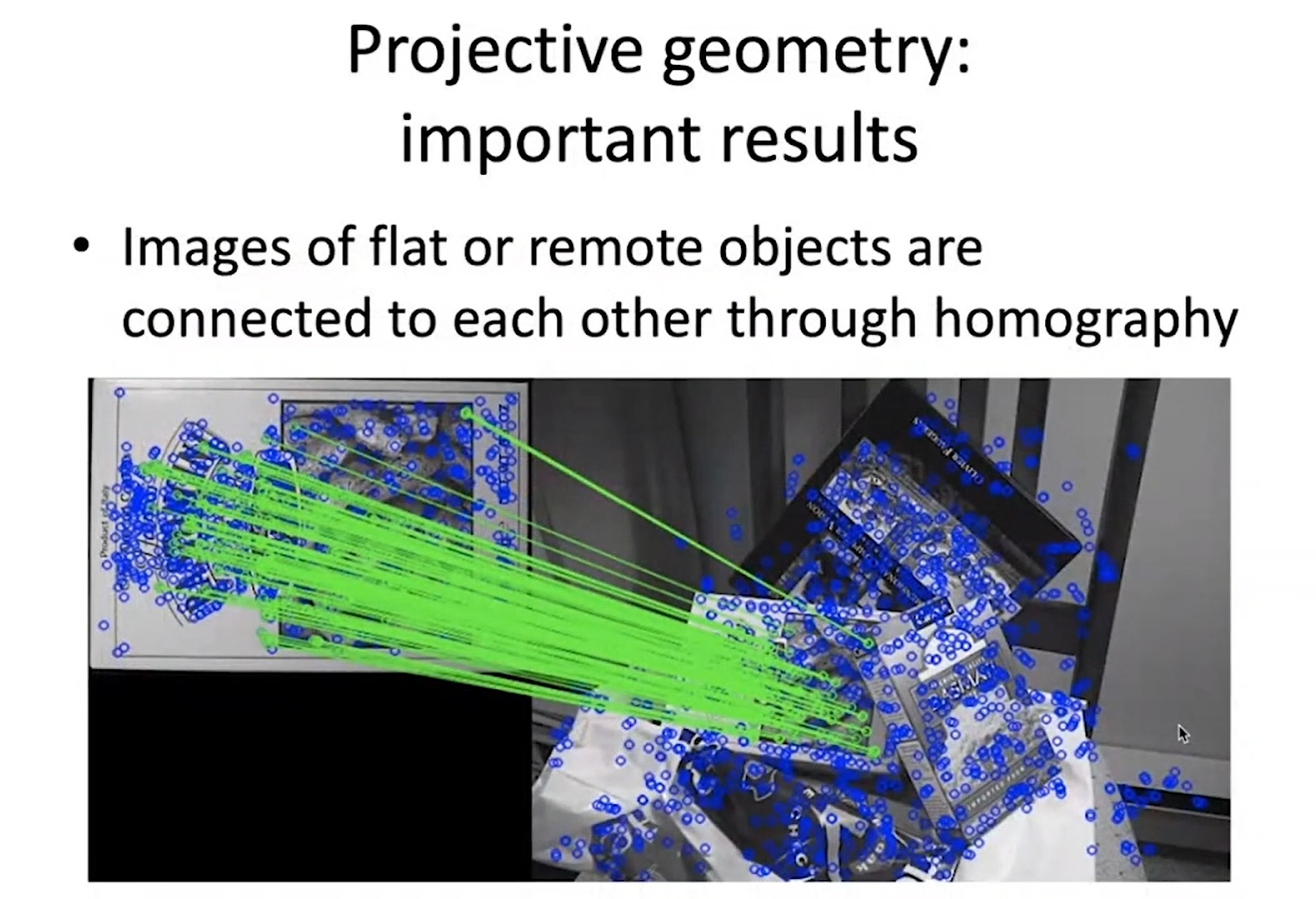
До возникновения компьютерного зрения задачи, которыми сейчас занимается Pinhole camera, решались областью проективной геометрии. Изучая эту научную сферу, мы получили множество важных наблюдений и открытий, причем довольно давно:

Если у нас есть изображение одного и того же плоского объекта с двух разных точек зрения, то эти изображения связаны друг с другом через преобразования демографии, у которого всего восемь параметров.
Задача калибрации камеры – была решена в 2000 годах с помощью принципа шахматной доски.
Задача PnP. Предположим, у нас есть известный объект, который должен взять робот на фабрике. Мы заранее отсканировали трехмерную форму и текстуру объекта, поэтому мы легко можем найти изображение пикселей текстуры и сопоставить трехмерные координаты. Задача состоит в том, чтобы понять, как найти положение этого объекта в системе координат, связанной с камерой. То есть, из мировой системы координат, где нам известны трехмерные положения точек (обычная система координат, связанная с объектом или со сканером, который снимал объект), мы хотим перейти в систему координат, связанную с камерой, чтобы точно знать, где находится сетка этого объекта в нашей камере. Эта задача также считается решенной; интересно то, что её решали больше 170 лет. Первые решения были опубликованы ещё в 1841 году, когда было доказано, что если между тремя точками на плоскости и в пространстве есть соответствие, то множество решений конечно, но не равно единице. Последний статьи на эту тему 2006-2011 года – это методы, которые находят PnP в явном виде, без оптимизации и без итеративных алгоритмов.

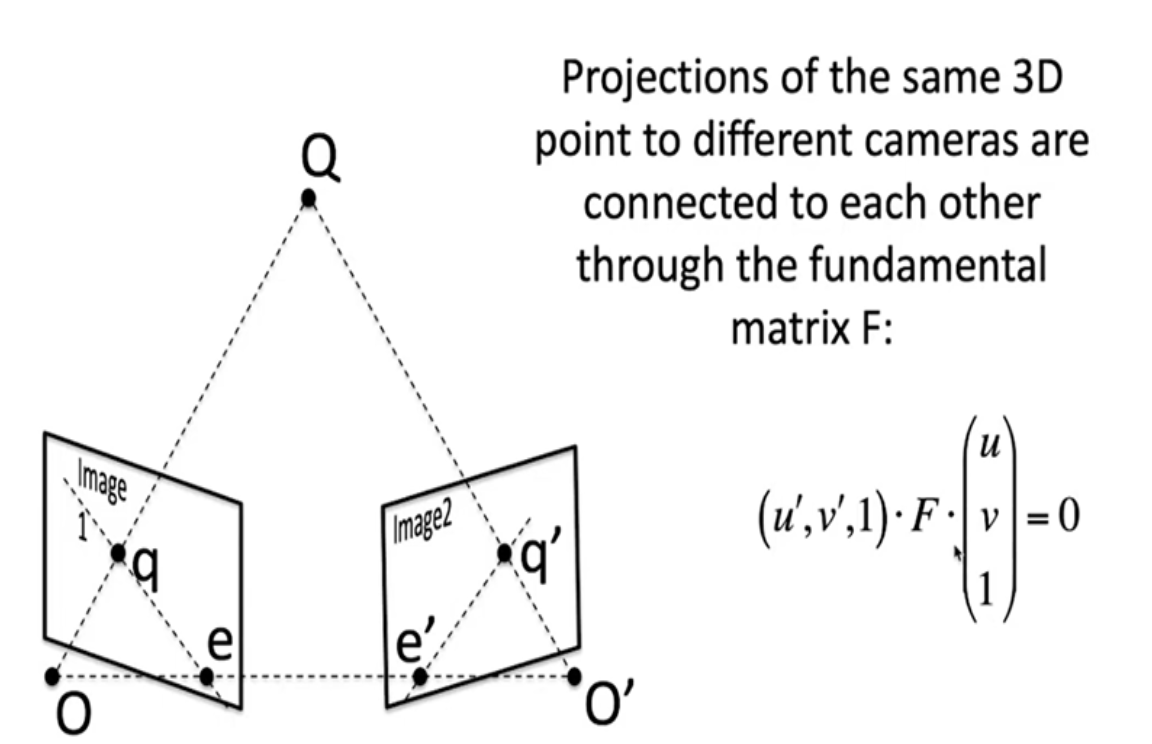
Если у нас есть две камеры, которые смотрят на одну и ту же трехмерную точку, и мы знаем проекцию этой точки на одном из двух изображений, но не знаем трехмерные координаты этой точки, то тогда на второй камере эта трехмерная точка может находиться на прямой линии, которая получается проектированием этого луча на вторую камеру. Соотношение между координатами двух пикселей, которым соответствует одна и та же трехмерная точка, задается следующим образом: u, v и u’, v’ – это координаты пикселей на левом и правом изображении, соответственно, F – это матрица 3×3, также известная как фундаментальная матрица. Если мы зафиксировали u’, v’, то получаем уравнение прямой линии относительно u, v. Фундаментальная матрица не зависит от трехмерной сцены, а зависит исключительно от расположения камер и их внутренних параметров.

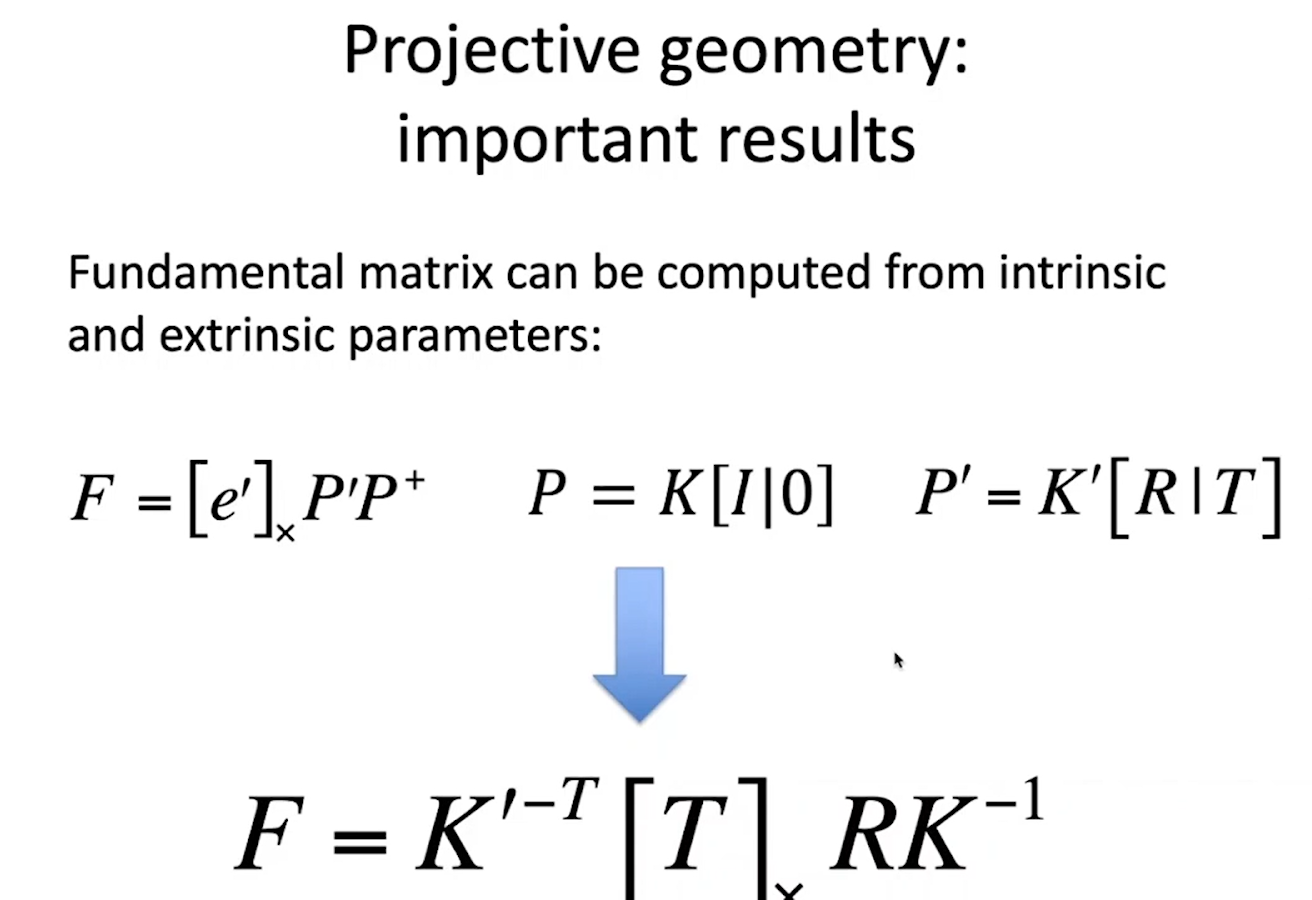
Фундаментальную матрицу можно выразить через матрицу проекции двух камер или, если нам известно их взаимное расположение, поворот и трансляция, то фундаментальная матрица зависит от них и от матриц внутренних параметров К и К”. Квадратные скобки и крест – это оператор, означающий векторное умножение на вектор Т. Если нам известна фундаментальная матрица, которую мы можем найти по изображениям, используя соотношение между пикселями, то по ней мы можем восстанавливать взаимное расположение камер.

Если мы знаем взаимное расположение камер и соответствие между пикселями, то мы можем сделать триангуляцию и, таким образом, получить стереозрение.

Стереозрение

Стереозрение – это широкая область, которая позволяет довольно точно восстанавливать положение трехмерных и текстурных объектов. Кроме быстрых алгоритмов в этой области есть и медленные, которые дают большую гладкость и корректность по границам – например, алгоритм Hirschmüller’а 2005 года. Также есть множество алгоритмов, которые основаны на глубоком обучении.

Проблемы, связанные со стереозрением, обычно состоят в том, что однородные области плохо подвергаются обработке, потому что, во-первых, внутри них не так просто найти соответствие, а во-вторых, если мы работаем с дешевыми камерами, то их сигнал снимается в разные моменты времени – в результате чего мы получаем некорректную сцену, если снимаем быстрое движение. То есть на двух камерах мы получим разные картинки. Поэтому для машинного зрения на фабриках используют global shutter – более дорогие камеры, которые снимают картинку в один и тот же момент по внешнему сигналу.

Точно по такому же принципу работает Face ID, только у него вместо одной из двух стереокамер используется инфракрасный прожектор. Таким образом, решается задача с однородными областями: мы как бы делаем их принудительно неоднородными.

Теорема о проективной реконструкции

Даже если взаимное расположение между камерами неизвестно, то мы по-прежнему можем найти соответствие между пикселями и фундаментальную матрицу. Есть теорема о проективной реконструкции, которая утверждает, что если нам неизвестны внутренние параметры камер, то реконструкция становится возможной только в точности до гомографии в P3. Гомография в P3 – это преобразование в R3, которое превращает куб в произвольный шестигранник. Плоскости остаются плоскостями, но параллельные плоскости уже могут быть непараллельными и так далее. Два решения, которые равны друг другу в точности до преобразования в P3, будут давать абсолютно одинаковые фундаментальные матрицы. Если мы знаем что-то про сцену, например, три системы параллельных линий в трехмерном пространстве, как на картинке выше, то мы можем убрать некоторое количество параметров и свести к реконструкции, когда параллельные линии в трехмерном пространстве будут параллельными. Поэтому, например, восстановить видео с Ютуба будет сложной задачей, но если по расположениям двух камер мы сможем восстановить систему с точностью до масштаба, то дальше мы можем попытаться восстановить все сцену.

SLAM

Один из примеров такого восстановления – SLAM, когда берут множество туристических изображений и по ним восстанавливают большую трехмерную сцену.

Давайте посмотрим поближе, как они это делают.

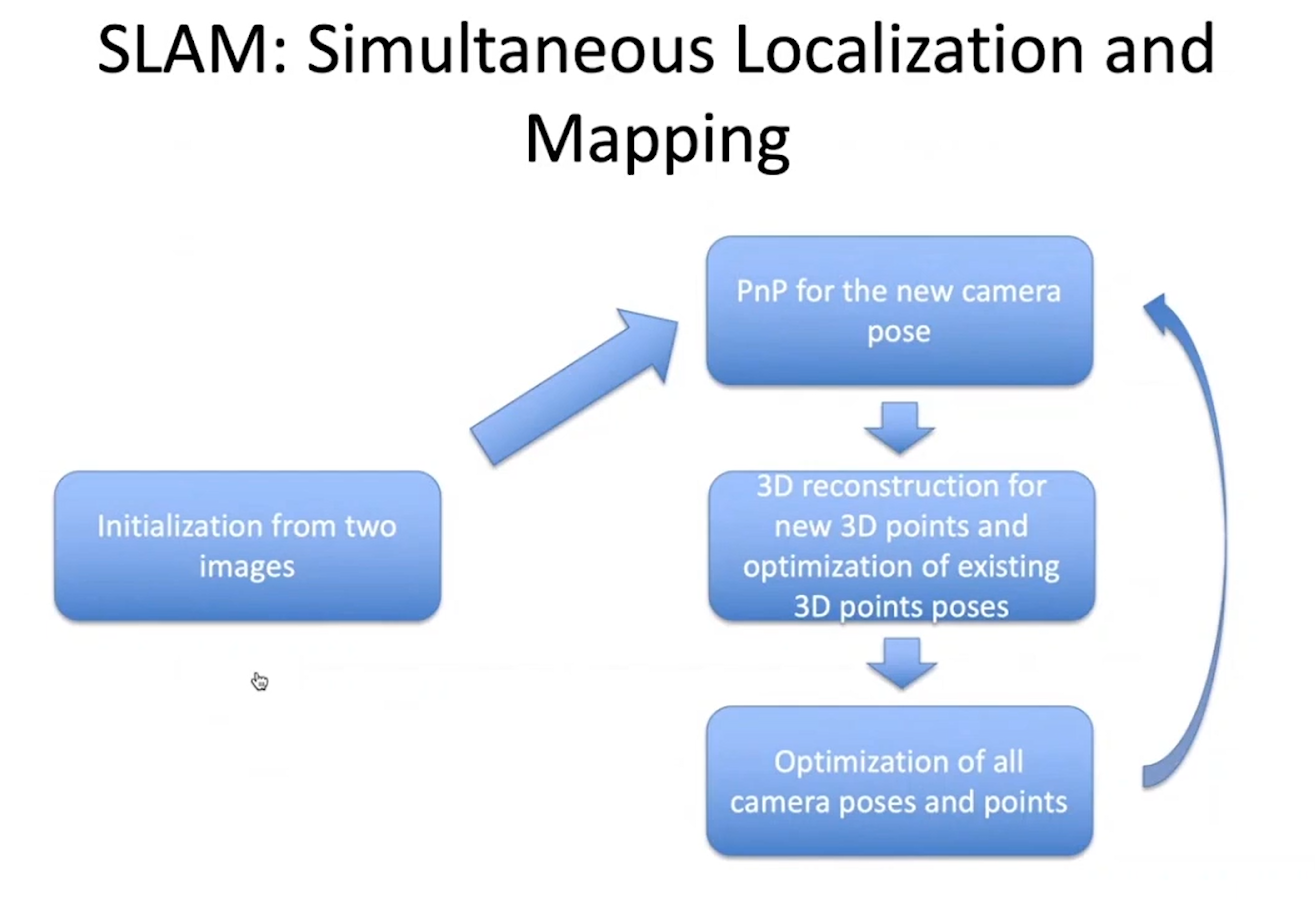
Идея любого SLAM довольно проста – мы берем два изображения, находим пиксельные соответствия внутри них и фундаментальную матрицу. Так как внутренние параметры камеры нам известны, то мы можем восстановить позу одной камеры относительно другой; после этого мы применяем триангуляцию и получаем трехмерные точки – те, для которых мы нашли соответствия.

Затем мы берем еще одно изображение, которое пересекается с первыми двумя, и ищем для него позу по соответствиям первых двух: поскольку у нас уже есть трехмерные точки, мы можем запустить PnP и найти позу. Как только мы находим её, то для тех точек, которые присутствуют на третьей и второй камере, но не присутствуют на первой (поэтому мы не знаем их трехмерные координаты), мы можем сделать триангуляцию, то есть, найти трехмерные координаты для новых точек.

Последний шаг в этой последовательности оптимизирует положение камер и точек – если у вас есть большое количество точек на сцене и небольшое количество положений камер, то вы можете использовать так называемый Schur complement trick, когда весь этот шаг сводиться к задаче с матрицами и решение этой задачи просто делится на камеры и трехмерные точки.

Вышеперечисленные ресурсы решают задачу восстановления трехмерной структуры по набору изображений. Решение требует определенных навыков в запуске, но, тем не менее, считается одним из лучших.

Аналогичные методы используются для фотогаллометрии, когда мы снимаем какой-то объект многими камерами и дальше помещаем этот объект в кино. Если у нас есть какие-то поляризационные фильтры, то также мы можем получить нужные нам поверхности.

Новые методы

Теперь давайте поговорим о новых методах, которые используют априорную информацию, например, класс объекта. Фактически, для того чтобы использовать какие-то методы машинного обучения для задач восстановления 3D, нам надо каким-то образом представлять трехмерную модель, потому что стандартные co-evolution networks работают с изображением и с абстрактными векторами. Есть несколько способов представления трехмерных изображений и помещения их в нейронные сети:

Параметрические модели.
Point-cloud.
Поверхности с одной и той же топологией.
Методы, основанные на вокселях, включая иерархические.
Непрерывные представления.
Neural Radiance Fields.

Параметрические модели

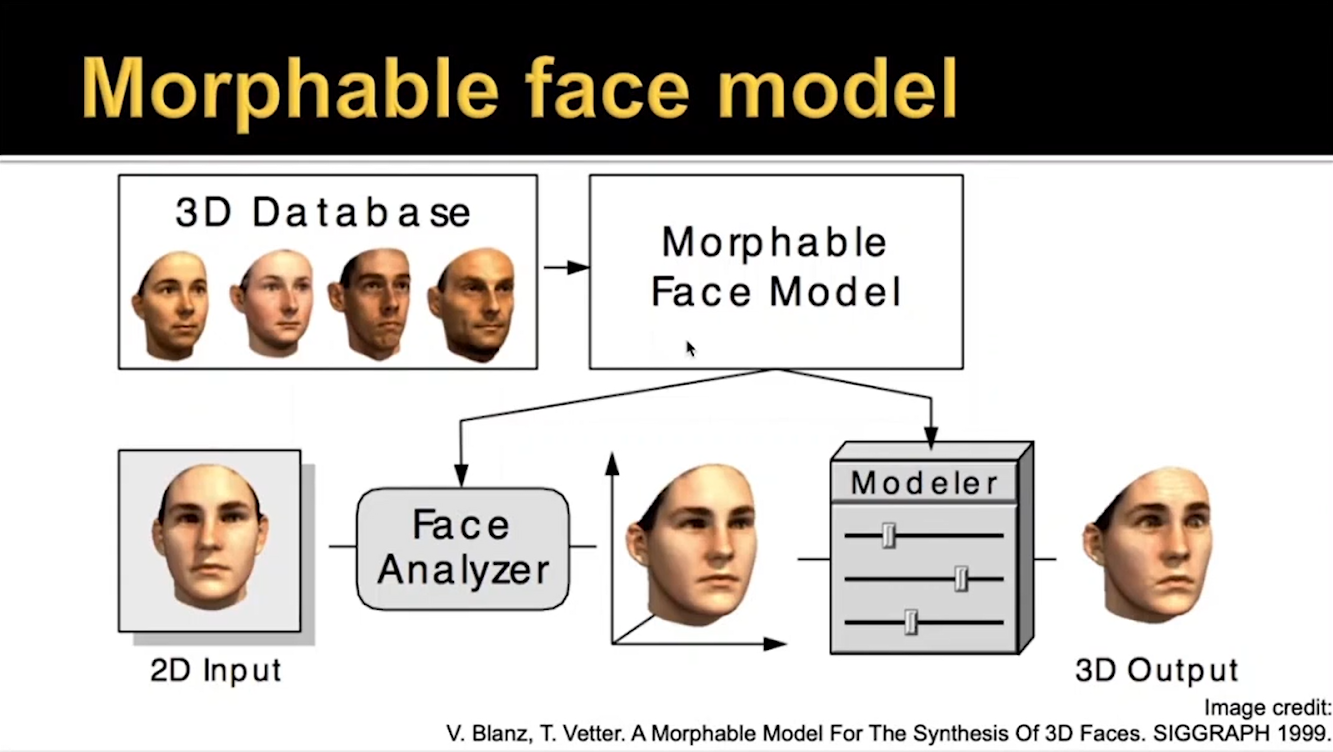
Начнем с параметрических моделей – выше представлена одна из работ, которая была сделана до того, как нейронные сети завоевали себе место в технологии компьютерного зрения. Исследователи брали сканы множества лиц, приводили их к единой системе координат и делали одну и ту же топологию. Далее они описывали текстуру и форму следующими формулами:

В этом случае можно делать отдельные коэффициенты, которые отвечают за личность человека и за выражение его лица. То есть модель позволяет коэффициентам добавлять веса и менять идентичность: например, если мы увеличиваем коэффициент таким образом, что модель отдаляется от средней модели, то получаем карикатуру – все черты лица подчеркивают отличие от средней модели.

Дальше было написано достаточно много работ, связанных с Morphable model для лиц, когда появились автоматические лэндмарки на лице, и соответственно, появилась возможность лучше строить соотношения между сканами и возможность предсказывать эти параметры.

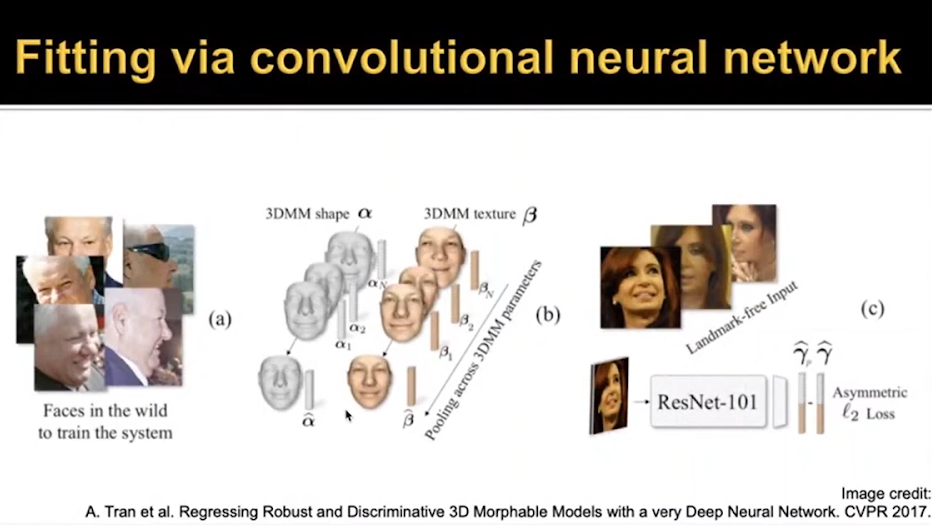
Здесь использовали ту же самую модель, единственное её отличие в том, что её тренировали на очень большом количестве лиц. Для каждой фотографии в этом исследовании получали трехмерную модель лица и на этом соотношении тренировали новую сеть. Они заметили, что при предсказании всех коэффициентов система часто тяготеет к среднему: это объясняется тем, что около начала координат больше точек; из-за этого теряется идентичность человека. Чтобы бороться с этим, они использовали следующую ассиметричную функцию:

В результате получался некий упрощенный набор параметров плюс положение лица, и для каждого параметра меняли коэффициенты, чтобы вычислить ошибку. В результате лица (а) описывали норму, а (с) получались асимметричными.

Непараметрические методы

Переходя к непараметрическим методам, мы начнем с баз данных, которые используются для их тренировки. Самые известные – это набор объектов Икеа (Ikea dataset), Pix3D и ShapeNet. В Pix3D использовали набор предметов Икеа и их изображения, получилось следующее:

Затем они размечали полученные объекты и запускали PnP, затем находили позы, регистрировали объекты и выбирали лучшие.

ShapeNet

ShapeNet – это набор 3D моделей, создан на основе двух источников: Trimble3DWarehouse и Yobi3D. Есть несколько статей, которые восстанавливают изображения по ShapeNet, первая из них – это MarrNet. Идея состоит в том, что в изображениях есть освещение, силуэт, глубина и прочие свойства 3D, которые можно использовать для тренировки:

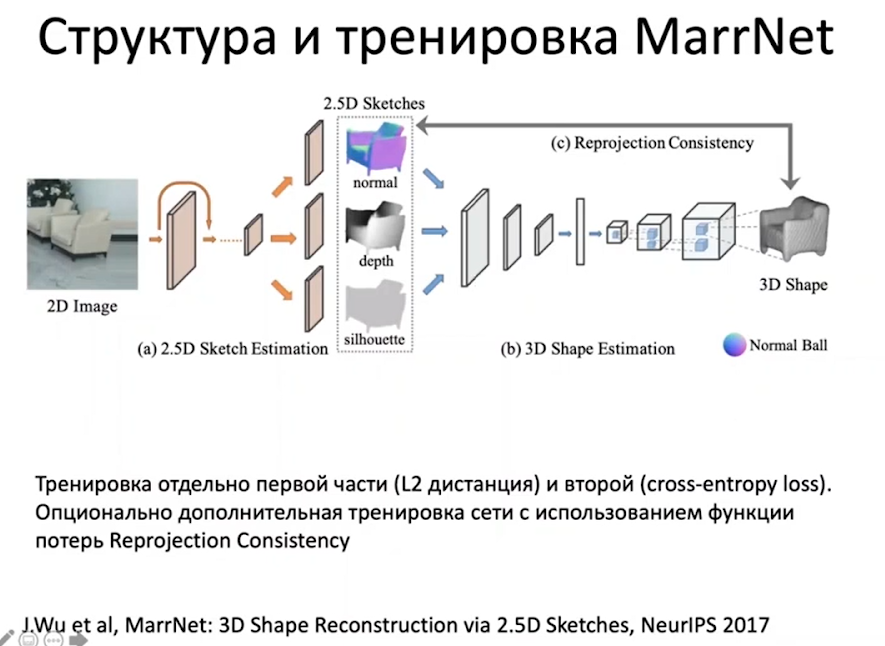
После того, как сеть натренировали на объекты, предсказывают функцию потерь: например, если у нас был предсказан воксель, то перед ним, на передней линии камеры, не должно быть ничего, то есть, все остальные воксели должны быть пустыми. И дальше вторую часть дотренировывают исключительно с помощью функции потерь.

Есть класс работ, которые используют для описания объекта трехмерные точки – нейронная сеть предсказывает вектор координат этих точек. В этом случае функция потерь – это любая дистанция, которая определена между двумя множествами неупорядоченных точек.

Также в работах подобного типа используется представление о поверхности через индикаторную функцию – оно называется неявным представлением, когда мы определяем функцию от трехмерной точки p:

Не стоит забывать и о методе дифференцируемого рендеринга – когда мы заявляем, что параметры сцены – это сетка, текстура и всё, что связано с освещением – и пытаемся построить такую модель рендеринга, которая была бы связана с изображением. Дальше мы считаем производные, чтобы понять, как считывать изображение.

В последнее время фурор в сфере производит набор методов Neural Radiance Fields. Суть состоит в том, что мы представляем трехмерную поверхность с помощью описания формы и radiance. То есть мы задаем не просто текстуру, а свет, который отражается от этой точки в определенном направлении, таким образом, учитывая тип поверхности. Используя такую модель, мы пытаемся тренировать ее по изображениям. Для представления формы поверхности используется модель, которая называется «объемная плотность», которая предсказывает вероятность того, что луч оборвется именно в этой точке: если 1 – значит, есть объект, если 0 – значит, пустое пространство. Таким образом, мы можем считать цвет конкретного пикселя, зная внутренние параметры камеры, выпуская луч и считая интеграл, который зависит от объемной плотности вдоль этого луча и от цвета в radiance модели в каждой из этих точек:

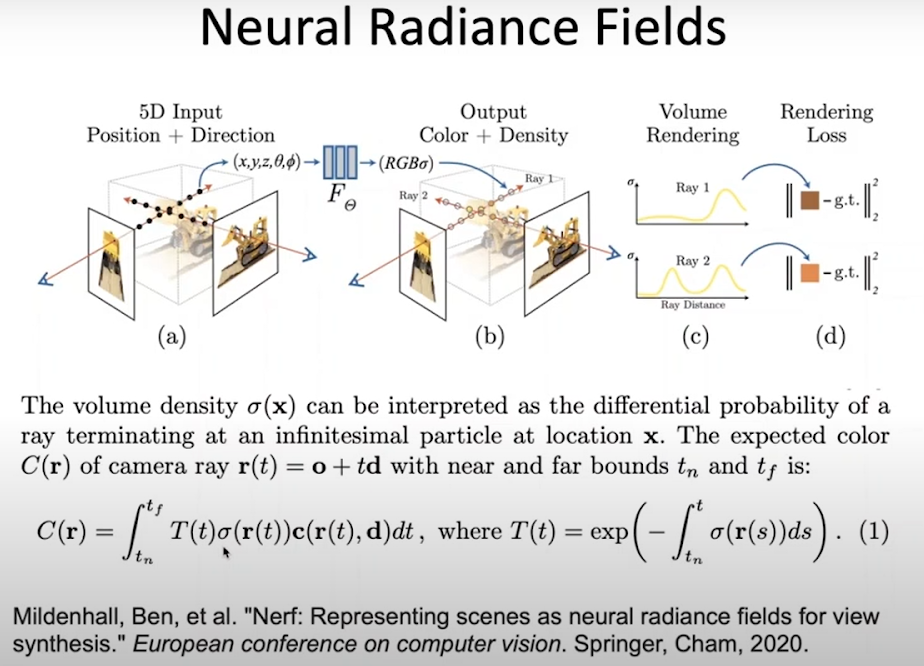
Этому можно обучать по изображениям без использования трехмерных структур.

Для того, чтобы получать более качественную модель, вместо того чтобы брать три координаты, применяется Positional encoding, когда к каждой координате применяется следующее преобразование:

Этот метода аналогичен тому, который используется в трансформерах.

Q&A:

Q: Недавно появился Object capture от Apple. В нем используется COLMAP, то есть какой-то классический способ?

А: Мы тестировали его и пришли к выводу, что это классическая фотогаллометрия. Результаты очень похожие.

Q: Как можно использовать NERF?

А: Сейчас такие стартапы пытаются сделать аналог 360 view, например, где на веб-сайте вы получаете объект, который можно покрутить. У меня есть вопросы к самой модели, потому что эта задача решается разными способами, например, через 360 фото. Я знаю, что один из стартапов решал задачу более классическим способом – по набору изображений синтезировал промежуточные модели. Лично мне NERF интересен тем, что это первая модель, которая позволяет строить модели без 3D. То есть вы можете сделать объект по набору изображений. В итоге получается более детализированная и информативная модель, которая учитывает спекулярные поверхности, в то время как COLMAP думает, что все поверхности диффузные и имеют цвет.

Q: Что полезного можно делать с помощью пользовательских камер, например, камеры телефона?

А: Внешняя камера телефона работает как фотогаллометрия – она недостаточно мощная, чтобы с её помощью сканировать объекты. Face ID, которая смотрит на пользователя вполне способна сканировать лицо, и её используют именно для этого.

Q: А не лучше ли качество LIDAR сенсоров, например?

А: Те, что предназначены для телефонов, конечно, несравнимы – в наших тестах у них было больше пропущенных точек, чем найденных, особенно на темных материалах. Также возникали проблемы с их сканированием. Мощные намного лучше, чем structured light, например, LIDAR на автомобилях могут работать и на десятки и на сотни метров, а на самолетах еще лучше.

По материалам открытого семинара Виктора Ерухимова «От COLMAP к NERF: обзор методов трехмерной реконструкции объектов по изображениям»‎, который прошел в Xperience.AI.